ضریب همبستگی چیست؟

در آمار و احتمالات، ضریب همبستگی یک مفهوم مهم است که نشان می‌دهد چقدر دو متغیر تصادفی با یکدیگر مرتبط یا همبسته هستند. در واقع، ضریب همبستگی نشان‌دهنده‌ی اندازه و جهت رابطه بین دو متغیر تصادفی است.

ضریب همبستگی بین دو متغیر معمولاً از -1 تا 1 مقدار می‌گیرد:

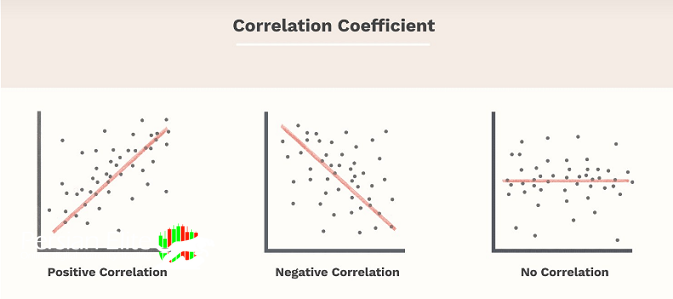
1. اگر ضریب همبستگی به سمت +1 نزدیک باشد، این نشان می‌دهد که دو متغیر در حالتی مثبتاً خطی و قوی با یکدیگر همبستگی دارند، به عبارت دیگر، هر افزایش در یکی از متغیرها به احتمال زیاد باعث افزایش مشابه در متغیر دیگر می‌شود.

2. اگر ضریب همبستگی نزدیک به صفر باشد، این نشان‌دهنده‌ی عدم وجود همبستگی خطی قوی بین دو متغیر است. با این حال، همبستگی غیرخطی ممکن است وجود داشته باشد.

3. اگر ضریب همبستگی به سمت -1 نزدیک باشد، این نشان می‌دهد که دو متغیر در حالتی منفی خطی و قوی با یکدیگر همبستگی دارند، به عبارت دیگر، افزایش یکی از متغیرها باعث کاهش مشابه در متغیر دیگر می‌شود.

ضریب همبستگی معمولاً با علامت "r" نمایش داده می‌شود. برای محاسبه ضریب همبستگی بین دو متغیر، از روش‌های مختلفی مانند روش پیرسون (برای متغیرهای پیوسته) و روش سپیرمن (برای متغیرهای ترتیبی) استفاده می‌شود.

جدیدترین و بروز ترین اخبار ارز دیجیتال را از پرشین الیت بخواهید

ضریب همبستگی (Correlation Coefficients)

ضریب همبستگی (Correlation Coefficient) یک مفهوم مهم در آمار و احتمالات است که نشان‌دهنده‌ی میزان و نوع ارتباط بین دو متغیر تصادفی است. این ضریب به ما اطلاعاتی درباره‌ی جهت و قدرت ارتباط بین دو متغیر را ارائه می‌کند. ضریب همبستگی معمولاً با علامت "r" نمایش داده می‌شود.

دو نوع اصلی از ضرایب همبستگی عبارتند از:

1. ضریب همبستگی پیرسون (Pearson Correlation Coefficient):
   این ضریب همبستگی برای اندازه‌گیری ارتباط بین دو متغیر پیوسته (متغیرهایی که می‌توانند مقادیر مختلف پیوسته به خود بگیرند) استفاده می‌شود. مقادیر این ضریب همبستگی بین -1 و 1 قرار دارند:

   - اگر r به سمت +1 نزدیک باشد، نشان‌دهنده‌ی ارتباط مثبت و خطی است.
   - اگر r به سمت -1 نزدیک باشد، نشان‌دهنده‌ی ارتباط منفی و خطی است.
   - اگر r به سمت 0 نزدیک باشد، نشان‌دهنده‌ی عدم وجود ارتباط خطی است.

2. ضریب همبستگی سپیرمن (Spearman Correlation Coefficient):
   این ضریب همبستگی برای اندازه‌گیری ارتباط بین دو متغیر ترتیبی (متغیرهایی که می‌توانند به ترتیب مقادیر مختلف را از خود بگیرند) استفاده می‌شود. این ضریب بر اساس رتبه‌بندی مقادیر داده‌ها عمل می‌کند.

هر دو نوع اصلی از ضرایب همبستگی به تاحدی از نویز و تغییرات تصادفی در داده‌ها تحت تأثیر قرار می‌گیرند، بنابراین ممکن است در مواقعی نتایج نادرستی ارائه دهند. همچنین، ضریب همبستگی تنها ارتباط خطی را اندازه‌گیری می‌کند و در مواردی که ارتباط غیرخطی وجود دارد، ممکن است به‌طور ناصحیح نتایج را تفسیر کند.

عوامل موثر بر correlation coefficient

ضریب همبستگی (Correlation Coefficient) بین دو متغیر می‌تواند تحت تأثیر مجموعه‌ای از عوامل مختلف قرار بگیرد. این عوامل می‌توانند تأثیر مثبت یا منفی بر روی مقدار و حتی تفسیر ضریب همبستگی داشته باشند. برخی از اصلی‌ترین عوامل موثر بر ضریب همبستگی عبارتند از:

1. نوع ارتباط: نوع ارتباط میان دو متغیر (خطی، غیرخطی، منفی، مثبت) می‌تواند بسیاری از تفاوت‌ها در مقدار ضریب همبستگی ایجاد کند. در صورتی که ارتباط میان دو متغیر غیرخطی باشد، ضریب همبستگی پیرسون ممکن است نتایج نادرستی ارائه دهد و در این موارد، استفاده از روش‌های دیگر مانند ضریب همبستگی سپیرمن توصیه می‌شود.

2. تغییرات انحراف معیار: اگر یکی از متغیرها دارای تغییرات بزرگی باشد و دیگری دارای تغییرات کمتری باشد، ممکن است ضریب همبستگی کمتری بین آن دو متغیر وجود داشته باشد.

3. پرت‌ها (Outliers): وجود پرت‌ها (داده‌های ناهنجار یا از دست رفته) می‌تواند تأثیر قابل توجهی بر روی ضریب همبستگی داشته باشد. پرت‌ها می‌توانند ارتباط را تغییر داده یا حتی ضریب همبستگی را به سمت مقدارهای غیرصفر سوق دهند.

4. نمونه‌برداری نامناسب: نحوه‌ی انتخاب نمونه و تعداد داده‌ها نیز می‌تواند تأثیر بر ضریب همبستگی داشته باشد. نمونه‌برداری نامناسب می‌تواند نتایج تحلیل را تحت تأثیر قرار داده و به نتایج نادرست منجر شود.

5. مقیاس متغیرها: تفاوت‌های در مقیاس متغیرها نیز می‌تواند تأثیر بر ضریب همبستگی داشته باشد. برای مثال، اگر دو متغیر از مقیاس‌های مختلف استفاده کنند، ضریب همبستگی ممکن است تحت تأثیر قرار گیرد.

6. اندازه نمونه: اندازه نمونه‌ای که برای محاسبه ضریب همبستگی استفاده می‌شود، می‌تواند تأثیر قابل توجهی داشته باشد. با افزایش اندازه نمونه، تخمین ضریب همبستگی معمولاً دقیق‌تر خواهد بود.

به طور کلی، تفسیر ضریب همبستگی باید با دقت به عوامل مختلف و شرایط محیطی که در تحلیل داده‌ها وارد می‌شوند، انجام شود. همچنین، برای تفسیر درست نتایج، می‌بایست با دانش کافی از مفاهیم آماری و تحلیل داده‌ها همراه باشید.

انواع روش های همبستگی Correlation

روش‌های مختلفی برای اندازه‌گیری همبستگی بین دو متغیر وجود دارند. در ادامه، به برخی از اصلی‌ترین روش‌های همبستگی اشاره خواهم کرد:

1. ضریب همبستگی پیرسون (Pearson Correlation Coefficient):
   این روش برای اندازه‌گیری ارتباط خطی بین دو متغیر پیوسته استفاده می‌شود. ضریب همبستگی پیرسون در بازه‌ی -1 تا 1 قرار دارد و میزان و نوع ارتباط خطی را نشان می‌دهد. اگر r به سمت +1 نزدیک باشد، ارتباط مثبت و خطی نشان می‌دهد؛ اگر به سمت -1 نزدیک باشد، ارتباط منفی و خطی؛ و اگر به سمت 0 نزدیک باشد، عدم وجود ارتباط خطی.

2. ضریب همبستگی سپیرمن (Spearman Correlation Coefficient):
   این روش برای اندازه‌گیری ارتباط بین دو متغیر ترتیبی (ترتیب‌ها یا رتبه‌ها) استفاده می‌شود. این روش مقادیر داده‌ها را به ترتیب‌ها تبدیل می‌کند و ارتباط بین ترتیب‌ها را اندازه‌گیری می‌کند. ضریب همبستگی سپیرمن نیز بین -1 و 1 قرار دارد.

3. ضریب همبستگی کندال (Kendall Tau Correlation Coefficient):
   این روش نیز برای اندازه‌گیری ارتباط بین دو متغیر ترتیبی مورد استفاده قرار می‌گیرد. ضریب همبستگی کندال نشان‌دهنده‌ی تطابق ترتیب‌ها و ارتباط بین آن‌ها است.

4. ضریب همبستگی بیسریال (Point-Biserial Correlation Coefficient):
   این روش برای اندازه‌گیری ارتباط بین یک متغیر دودویی (دارای دو دسته) و یک متغیر پیوسته استفاده می‌شود. این ضریب معمولاً بین -1 و 1 قرار دارد و میزان ارتباط بین متغیرها را نشان می‌دهد.

5.ضریب همبستگی رنگو (Rank Correlation Ratio - RCR):
   این روش نسبت به تغییر در توزیع متغیرها نسبت به توزیع اولیه آن‌ها حساس است و برای اندازه‌گیری ارتباط میان ترتیب‌های دو متغیر استفاده می‌شود.

همچنین، در موارد خاص دیگری مانند روش‌های همبستگی مخصوص داده‌های زمانی (مانند ضریب همبستگی میانگین متحرک) و داده‌های متعامل (مانند ضریب همبستگی متعامل) نیز وجود دارد. هر روش دارای ویژگی‌ها و محدودیت‌های خود است و انتخاب مناسب‌ترین روش به توجه به نوع داده‌ها و هدف تحلیل بستگی دارد.

در همبستگی دو نماد چه نکاتی وجود دارد؟

در مطالعه همبستگی بین دو نماد (متغیر)، چند نکته مهم وجود دارد که باید به آن‌ها توجه کرد:

1. نوع داده‌ها: مهم است که بدانید داده‌هایی که با آن‌ها کار می‌کنید، چه نوعی هستند. آیا داده‌ها پیوسته هستند یا مثلاً ترتیبی؟ این انتخاب نوع مناسب از روش‌های همبستگی را تحت تأثیر قرار می‌دهد.

2. تعداد داده‌ها: تعداد داده‌های موجود نیز تأثیر مهمی بر دقت و قوت تحلیل همبستگی دارد. تعداد داده‌های کم ممکن است باعث ایجاد نتایج ناپایدار یا ناصحیح شود.

3. توزیع داده‌ها: بررسی توزیع داده‌ها مهم است. اگر داده‌ها از توزیع نرمال پیروی نمی‌کنند، ممکن است نتایج همبستگی تحت تأثیر قرار گیرند.

4. پرت‌ها (Outliers): وجود داده‌های پرت می‌تواند تحلیل همبستگی را تحت تأثیر قرار دهد. پرت‌ها می‌توانند تاثیر غیرمنطقی در مقدار و جهت همبستگی داشته باشند.

5. قوت همبستگی: بررسی قدرت همبستگی مهم است. ضریب همبستگی خود به تنهایی کفایت نمی‌کند؛ می‌بایست به همراه بررسی زاویه‌ی شیب منحنی رگرسیون یا انحرافات از میانگین نیز در نظر گرفته شود.

6. تفسیر: تفسیر نتایج همبستگی بسیار مهم است. اگرچه ضریب همبستگی اندازه‌گیری‌ای از ارتباط بین دو نماد است، این ارتباط ممکن است علتی نداشته باشد یا ممکن است توسط عوامل دیگر تبدیل شود.

7. غیرخطی‌بودن ارتباط: ضریب همبستگی معمولاً فقط ارتباط‌های خطی را اندازه‌گیری می‌کند. اگر ارتباط غیرخطی باشد، نتایج ممکن است نادرست باشند.

8. تاثیر نمونه‌برداری: نحوه‌ی انتخاب نمونه و تعداد داده‌ها نیز تأثیر مهمی بر نتایج همبستگی دارد.

9. زمان و دوره: اگر داده‌ها زمانی هستند، توجه به دوره‌ها و تغییرات ممکن است مهم باشد. ارتباط ممکن است در طول زمان تغییر کند.

10. سهم تصادفی: باید مطمئن شوید که همبستگی نتیجه‌ی تصادفی نیست و واقعیت دارد.

در کل، در تحلیل همبستگی، دقت و مراعات اصول آماری مهم است تا نتایج دقیق‌تر و قابل اعتمادتری حاصل شود.

کاربرد correlation coefficient در ترکیب پرتفوی

در ترکیب پرتفوی (Portfolio Management)، ضریب همبستگی (Correlation Coefficient) یکی از ابزارهای مهم است که در ارزیابی و مدیریت ریسک و عملکرد پرتفوها مورد استفاده قرار می‌گیرد. ضریب همبستگی در این حوزه دارای کاربردهای متعددی است:

1. تنوع پرتفو: ضریب همبستگی به مدیران پرتفوی کمک می‌کند تا متغیرهای مختلفی با درجه‌های مختلف از ارتباط میان دارند. با استفاده از دارا بودن دارایی‌های با ضریب همبستگی مختلف، می‌توان پرتفوی تنوع‌پذیر و کاهش ریسک ایجاد کرد.

2. تعیین ترکیب دارایی‌ها: در پرتفوهای مختلف، انتخاب ترکیب دارایی‌ها (سهام، اوراق بهادار، ملک، نقدینگی و غیره) مهم است. ضریب همبستگی به مدیران پرتفوی کمک می‌کند تا دارایی‌هایی را که ارتباط کمتری با یکدیگر دارند، با یکدیگر ترکیب کنند تا ریسک کلی پرتفو کاهش یابد.

3. مدیریت ریسک: ضریب همبستگی به مدیران پرتفو کمک می‌کند تا اندازه‌گیری کنند که دارایی‌های پرتفو چقدر با یکدیگر مرتبط هستند. اگر دارایی‌ها با هم همبستگی بالایی داشته باشند، در مواقع رخ دادن افت قیمت یک دارایی، احتمال افت قیمت دارایی‌های دیگر نیز افزایش می‌یابد. از این رو، ترکیب دارایی‌هایی با ضریب همبستگی کم می‌تواند ریسک کلی پرتفو را کاهش دهد.

4. پیش‌بینی عملکرد: ضریب همبستگی به مدیران پرتفو کمک می‌کند تا پیش‌بینی کنند که در شرایط مختلف بازار، پرتفو چگونه عملکرد خواهد داشت. با تحلیل ارتباط بین دارایی‌ها و تغییرات در بازار، می‌توان عملکرد پرتفو در آینده را براحتی پیش‌بینی کرد.

5. بهینه‌سازی پرتفو: ضریب همبستگی به مدیران پرتفو کمک می‌کند تا دارایی‌هایی را با هم ترکیب کنند که در کل باعث کمینه کردن ریسک و حداکثر کردن بازده پرتفو می‌شوند. بهینه‌سازی پرتفو با استفاده از ضریب همبستگی و سایر اطلاعات مالی و اقتصادی انجام می‌شود.

در کل، ضریب همبستگی یکی از ابزارهای مهم در ترکیب پرتفو است که به مدیران مالی کمک می‌کند تا پرتفوهای متنوع، بازده بالا و ریسک کمتر را ایجاد کنند.

مزایا و معایب  correlation-coefficient

مزایا:

1. اندازه‌گیری ارتباط: ضریب همبستگی به‌طور کمی اندازه‌گیری ارتباط بین دو متغیر را ارائه می‌دهد. این اندازه‌گیری میزان قوت و جهت ارتباط را نشان می‌دهد.

2. تشخیص رابطه‌های مهم: با استفاده از ضریب همبستگی، می‌توان روابط مهم میان متغیرها را شناسایی کرد. این می‌تواند به تصمیم‌گیری‌ها و تحلیل‌های مدیریتی کمک کند.

3. مدیریت ریسک: در ترکیب پرتفو و سایر روش‌های مدیریت سرمایه، ضریب همبستگی به مدیران کمک می‌کند تا دارایی‌هایی را با هم ترکیب کنند که در کل باعث کاهش ریسک مالی شود.

4. پیش‌بینی: با تحلیل ارتباط بین داده‌ها، می‌توان به صورت نسبی پیش‌بینی کرد که چگونه تغییرات در یک متغیر تاثیری روی متغیر دیگر خواهد داشت.

5. ارزیابی مدل‌ها: در تحلیل‌های رگرسیونی و مدل‌سازی، ضریب همبستگی می‌تواند به ارزیابی عملکرد مدل و تاثیرات متغیرها کمک کند.

معایب:

1. ارتباط غیرخطی: ضریب همبستگی معمولاً ارتباط‌های خطی را اندازه‌گیری می‌کند و برای ارتباط‌های غیرخطی به‌طور دقیق نمی‌تواند مناسب باشد.

2. تأثیر پرت‌ها: وجود پرت‌ها می‌تواند تأثیر قابل توجهی بر ضریب همبستگی داشته باشد و نتایج را تحت تأثیر قرار دهد.

3. نمونه‌برداری نامناسب: نمونه‌برداری نامناسب می‌تواند نتایج را تحت تأثیر قرار داده و اطلاعات غلطی ارائه دهد.

4. علل تصادفی: ضریب همبستگی به تنهایی نمی‌تواند علل ارتباط بین دو متغیر را تعیین کند. ممکن است ارتباط تصادفی باشد یا به علل دیگر بازگردد.

5. تاثیر مقیاس متغیرها: مقیاس متغیرها می‌تواند تأثیر قابل توجهی بر ضریب همبستگی داشته باشد.

در کل، استفاده از ضریب همبستگی باید با دقت و با در نظر گرفتن محدودیت‌ها و شرایط مختلف صورت پذیرد. همچنین، ترکیب ضریب همبستگی با سایر روش‌ها و معیارها می‌تواند به نتایج دقیق‌تر و معتبرتری منجر شود.

نتیجه گیری

در نتیجه، ضریب همبستگی یک ابزار مهم در تحلیل داده‌ها و مدیریت پرتفوی است که به ما اطلاعاتی ارائه می‌دهد تا بتوانیم ارتباط میان دو متغیر را اندازه‌گیری کنیم. با استفاده از ضریب همبستگی، می‌توانیم میزان تغییرات متغیرها و تاثیر یکدیگر را درک کنیم، تنوع پرتفو را افزایش دهیم، عملکرد پرتفو را پیش‌بینی کنیم و ریسک‌های مالی را مدیریت کنیم. با این حال، باید به محدودیت‌ها و شرایط مختلف نیز توجه داشته باشیم. ضریب همبستگی ممکن است برای ارتباط‌های غیرخطی مناسب نباشد، تاثیر پرت‌ها را داشته باشد و نمونه‌برداری نامناسب باعث نتایج نادرست شود. به طور کلی، برای استفاده مؤثر از این ابزار، نیازمند ترکیب آن با سایر روش‌ها و تجزیه و تحلیل دقیق‌تر داده‌ها هستیم.

پرشین الیت ، کلید ورود شما به دنیای ارز دیجیتال.با پرشین الیت ، جدیدترین سیگنال های ارز دیجیتال ، فارکس و فیوچرز در دستان شما قرار دارد